Historia de la ecuación polinómica de tercer grado
Todos hemos resuelto alguna vez una ecuación de segundo grado con la conocida fórmula. Pero casi nunca hemos utilizado una fórmula para las ecuaciones de tercer grado, de cuarto, o de grado superior
hablamos sobre la historia que rodeó al descubrimiento del método para resolver ecuaciones cúbicas
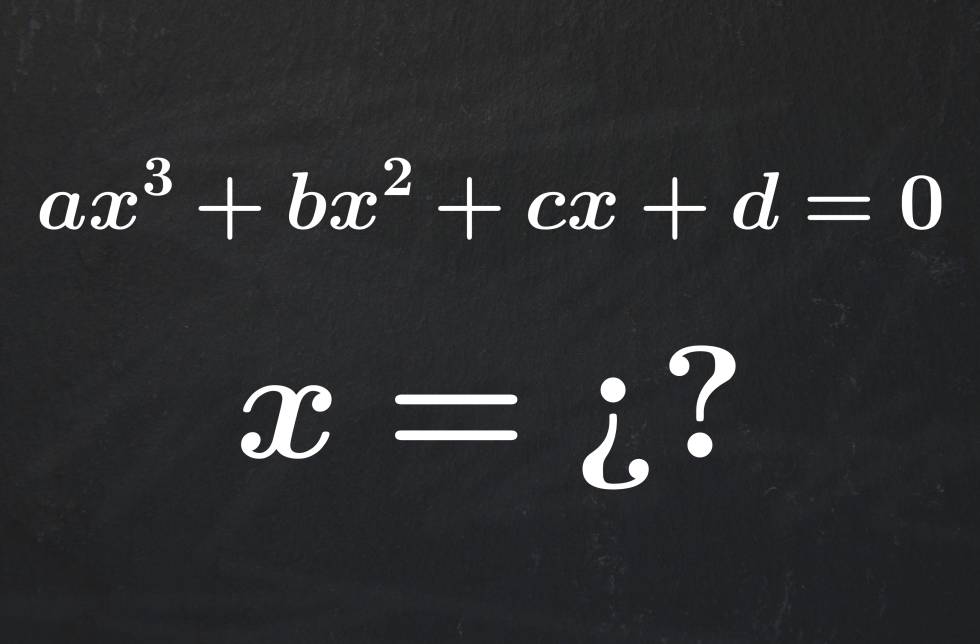
los métodos de resolución de estas ecuaciones polinómicas tienen una gran importancia dentro de esta parte de nuestra formación matemática.
lo primero que se tiene en cuenta es el grado de dicha ecuación. Las ecuaciones de grado 1 son sencillas de resolver (operar, separar términos y despejar), y para las de grado 2 tenemos una fórmula
Nuestra historia se sitúa en el siglo XVI y tiene como protagonistas principales a Niccolo Fontana (apodado Tartaglia por ser tartamudo), Girolamo Cardano,
en aquella época se expresaban de estas tres maneras, x3+px=q , x3=px+q y x3+q=px, y cada una tenía su propio método de resolución
Para resolver la cúbica general x3+mx2+nx=r. Esta ecuación puede reducirse fácilmente a una del tipo x3+px=q, por lo que solamente haría falta resolver ésta. Sus soluciones vienen dadas por la siguiente expresión:
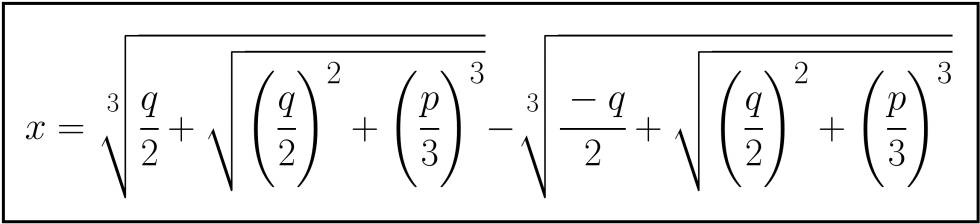
Aunque parece que solamente tenemos un valor, en realidad esta expresión representa los tres valores de las tres soluciones de la cúbica general
Niccoló Fontana:(Brescia, actual Italia, 1499 - Venecia, 1557) Matemático italiano. ... Ya adulto, se ganó la vida como profesor itinerante (según permiten conocer sus obras, vivió en Verona, Mantua y Venecia) y a través de su participación en concursos matemáticos.
Gerolamo Cardano: (Jérôme Cardan; Pavía, actual Italia, 1501 - Roma, 1576) Matemático italiano. Se graduó en la Universidad de Pavía y se doctoró en medicina (1526) en la de Padua. ... Ese mismo año fue admitido en la facultad de medicina, de la que al poco fue nombrado rector.
Comentarios
Publicar un comentario